Máquina de Turing, Decidibilidade e o Problema da Parada

Se você se acha o “bam bam bam” da computação mas nunca ouviu falar do Problema da Parada, não tem ideia do que é decidibilidade e muito menos uma Máquina de Turing, então eu sinto desapontá-lo porque, na verdade, ainda tem muito chão pela frente…

Mas não se preocupe, porque eu trago 2 notícias que vão mudar a sua vida!

A primeira (e mais chocante) é a de que a grande maioria dos problemas não tem solução. A segunda (e a melhor) é que nunca ter ouvido falar disso é um “problema” que nós vamos resolver agora com este artigo!

Não se convenceu? Bom, dá só uma olhada nas 3 perguntinhas abaixo e veja se elas não te deixam, no mínimo, intrigado…

Você sabia que é impossível garantir que…

• um antivírus jamais executa código malicioso?
• um determinado compilador produz o código mais rápido possível?
• dois parsers diferentes aceitam exatamente a mesma linguagem?

Reflita sobre essas perguntas… Você duvida disso?

Acontece que todos esses problemas são, na verdade, exemplos disfarçados do Problema da Parada, cuja insolubilidade já foi provada.

É por isso que entender o Problema da Parada e suas implicações é tão importante: para que você não perca tempo tentando resolver coisas que simplesmente não tem solução!

Para você entender de uma vez por todas esse tal “Problema da Parada”, eu começo este artigo contando da onde ele veio e tudo o que estava rolando na época em que Turing teve uma sacada brilhante que, literalmente, revolucionou o mundo.

Em seguida, eu explico o que é uma Máquina de Turing, como ela funciona e para que serve. Finalmente, nós usamos essas máquinas para esboçar uma prova do Problema da Parada e do Entscheidungsproblem.

EntscheisQUEM?

Calma que isso não foi um espirro… .

Só respira fundo e vem comigo que você já vai entender tudo “tin tin por tin tin”!

Vá direto ao assunto…

• Contexto histórico
• A Máquina Universal de Turing
• O Problema da Parada
• Resolvendo o Enscheidungsproblem
• Conclusão

Contexto histórico

Tudo começou em 1900 quando o matemático do chapéu mais maneiro da época, David Hilbert, resolveu fazer uma lista com os 23 maiores problemas em aberto do século.

Estes problemas ficaram conhecidos como os Problemas de Hilbert, e muitos deles estão sem solução até os dias de hoje.

Neste artigo, nós estamos interessados, especificamente, no segundo problema de Hilbert.

Hilbert foi, na verdade, bem ganancioso ao propor este problema: ele queria uma prova de que a matemática era consistente e completa.

Consistente significa que não é possível derivar absurdos como \(0 = 1\). Se isso fosse possível, todos os números virariam 0. Por exemplo, \(n \times 1 = n\), então, por hipótese, \(n \times 0 = n\), logo \(n = 0\).

E para quê serviria uma matemática que só tem 0? Já imaginou o mundo se só existisse o número 0? Provavelmente ainda estaríamos morando nas cavernas se fosse assim.

Por outro lado, a matemática ser completa significa que existe uma solução para todos os problemas que você conseguir expressar matematicamente.

A esta altura, você talvez esteja se questionando o seguinte:

Como assim nós usamos a matemática por milênios e ainda não provamos que a própria matemática está correta?

Pois é amigão, como até então não existia um formalismo para garantir que as matemática era correta, os matemáticos utilizavam suas ferramentas sem saber, ao certo, se elas podiam de fato ser utilizadas.

Eu sei que é estranho. Afinal, garantir que a corretude das ferramentas para que elas possam ser utilizadas faz parte da essência da matemática, ou antes, faz parte da essência da lógica!

Mas então, como é que fica a matemática em si?

Pois é, não fica!

Como assim?

Bem, em 1931, Kurt Godël apareceu com a resposta para esta pergunta, gerando um dos resultados mais chocantes da matemática…

Ao contrário do que todos esperavam, ele provou que se a matemática for consistente, então ela não é completa.

Ou seja, vamos aceitar por um momento que a matemática é consistente.

Se a matemática é consistente, então existem problemas por aí que podem ser enunciados mas que não podem ser resolvidos.

Agora considere, como exemplo, a seguinte frase, usada por Godël para provar que a matemática é consistente:

Este enunciado não pode ser provado.

Construindo esta frase no sistema axiomático em questão, tem-se um enunciado cuja prova implica em uma contradição, ou seja, se o sistema puder provar tudo (inclusive este enunciado), então ele é inconsistente.

Fala sério, o cara era um gênio, né?

Tanto é que Godël era brother de Einstein.

Esse resultado ficou conhecido como o Teorema da Incompletude de Godël.

Tá beleza… Existem problemas por aí que não tem solução. Ok, podemos viver com isso… Mas será que é possível olhar para um problema e responder de antemão: tem como resolver esse amiguinho? Em um linguajar mais formal: é possível decidir se um enunciado de lógica de primeira ordem pode ser provado?

Embora essa pergunta tenha vindo um pouquinho mais tarde, em 1928, ela era parte do Segundo Problema de Hilbert e ficou conhecida como Entscheidungsproblem que, em alemão, significa Problema da Decisão.

E é aí que entra o Benedict Cumberbatch Alan Turing e o Problema da Parada.

Talvez você já tenha ouvido falar dele, mas Alan Turing foi o cara que revolucionou o mundo criando o conceito de computador aos 24 anos de idade “só” (ênfase nas aspas) para resolver o Problema da Decisão.

Enquanto isso, aos meus 24 anos, cá estou eu escrevendo textos no Facebook…

Mas enfim, Alan Turing, recém graduado em Cambridge, formalizou o conceito de computação em seu paper: On the computable numbers with an application to the Entscheidungsproblem — em 1936, de forma completamente independente e sem supervisão.

A ideia que Turing descreveu nesse paper é, na realidade, bem simples…

Imagine uma máquina que possui uma fita infinita. Esta máquina pode:

• Escrever na fita infinita
• Ler da fita infinita
• Mover a fita infinita.

Pronto, por incrível que pareça, uma Máquina Universal ou Máquina de Turing é só isso mesmo, e é sobre ela que nós falaremos já, já!

O mais interessante dessa história toda é que, exatamente no mesmo ano que o artigo de Turing foi publicado, Alonzo Church, de Princeton (EUA), também resolveu o Entscheidungsproblem, porém usando uma abordagem completamente diferente da de Turing…

Church inventou um outro formalismo computacional chamado Cálculo Lambda.

Ao saber do trabalho de Turing, um de seus professores, Newman, imediatamente mandou uma carta para Church pedindo que recebesse Turing em Princeton para que eles trabalhassem juntos.

Em 1937, Turing começou a trabalhar com Church e, juntos, eles provaram a equivalência de seus trabalhos, que ficou conhecida como a Tese de Church-Turing.

Infelizmente, a galera de Princeton não deu a devida atenção ao fato de que tinha uns caras que resolveram o Entscheidungsproblem. Provavelmente o pessoal estava muito ocupado paparicando o Einstein, que ficava logo ali no final do corredor.

Em artigos futuros, eu certamente entrarei em mais detalhes sobre o Cálculo Lambda.

Por enquanto, só vou dizer que as máquinas de Turing proveem uma ideia muito mais natural de computabilidade, com a solução sendo construída passo-a-passo. Ah, você não concorda? Então me explica ali embaixo nos comentários porquê, mas venha com bons argumentos porque o próprio Church admitiu isso…

A Máquina Universal de Turing

Chega de lenga lenga, vamos falar da Máquina Universal.

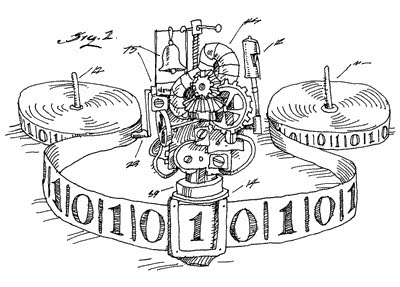
A primeira coisa que você precisa saber sobre a Máquina Universal é que ela pode ser configurada para realizar os mais diversos cálculos.

Por exemplo, suponha que você queira computar a função quadrado, que matematicamente falando pode ser definida como \(f(x) = x^2\).

Para fazer isso, em teoria, basta escrever o número o qual você quer calcular o quadrado em alguma posição da fita infinita, programar a máquina para realizar as operações necessárias e ligar a máquina. Ao final, quando a máquina parar, o resultado da computação pode ser lido da fita na posição programada.

Parece simples, né?

Mais ou menos… A formalização disso é um pouco cabeluda, mas fica o convite para que você estude todos os detalhes sórdidos em um curso de Teoria da Computação.

Turing teve uma base matemática muito boa em Cambridge, trabalhando em sua graduação com teoria dos grupos, tópico que estava na moda na época.

O Problema da Parada

Beleza então, temos uma máquina universal, inserimos uma entrada e esperamos até ela parar e checamos a saída.

Até aí tudo bem, certo?

Errado! Quem garante que a máquina vai parar?

Embora existam alguns problemas para os quais a máquina realmente não deve parar, como o cálculo de todos dígitos de \(\pi\), a capacidade de olhar para a máquina e determinar se algum dia ela vai parar é o que define o Problema da Parada.

Agora que você já sabe o que é o Problema da Parada, acho que eu já posso terminar o artigo aqui, né?

Na verdade, posso não! Porque agora é que as coisas ficam divertidas…

Sabe por quê?

Porque não tem como você olhar para a máquina e dizer se ela vai parar ou não.

É claro que você não se convence fácil assim, né? E esse é o espírito dos verdadeiros matemáticos… O espírito que diz: “Ah é? Então PROVA!”.

Então se prepara porque eu vou te dar uma ideia da prova… Preparado?

Assuma que existe uma Máquina Oráculo que recebe duas entradas:

1. Uma máquina universal qualquer;
2. Uma entrada para a máquina acima.

Calma lá, Pedro! Como assim uma máquina que recebe outra máquina como entrada?

Ué cara, tu acha que um compilador é o quê? Um compilador nada mais é do que um programa que recebe outro programa como argumento…

Tá, mentira, você me pegou… Um compilador, na verdade, é um programa que recebe o código de outro programa como argumento, e não o programa em si.

Mas é exatamente isso que estamos fazendo aqui: passando a codificação de uma máquina como entrada para outra máquina.

A função da Oráculo é olhar para esta outra máquina, analisar a entrada que foi passada e, de alguma forma, decidir se a máquina recebida vai parar em algum momento ao ser executada com esta entrada.

Como a Oráculo realiza a proeza de tomar essa decisão?

Não sei!

Se você voltar alguns parágrafos você vai ver que eu falei assuma que esta máquina existe, pois ainda não sabemos se tal máquina existe ou pode existir.

Ok, então vamos tentar mostrar que é impossível existir uma Oráculo…

Para isso, nossa estratégia será a seguinte: vamos seguir uma sequência de passos válidos e, se chegarmos em algum absurdo, então a única coisa possivelmente errada será a hipótese de que a Oráculo existe.

Agora vem a parte complicadinha, aperte o cinto…

Vamos construir uma máquina \(P\) (Oráculo) que recebe duas entradas:

1. Uma máquina universal \(Q\);
2. Uma entrada \(i\) para \(Q\).

O que \(P\) faz é o seguinte:

• Se \(Q\) parar com a entrada \(i\), então entre em loop.
• Se \(Q\) não parar com a entrada \(i\), então pare.

Mas o que acontece se passarmos para \(P\) a própria máquina \(P\)? Em outras palavras, o que acontece se \(Q = P\)?

E esse é o pulo do gato da prova, ou seja:

• Se \(P\) parar com a entrada \((P, i)\), então entre em loop.
• Se \(P\) não parar com a entrada \((P, i)\), então pare.

Pronto, chegamos a um absurdo: se \(P\) parar, então \(P\) entra em loop, e se \(P\) entrar em loop, então \(P\) para?!?!

Esta contradição indica que a máquina Oráculo não pode existir.

​\(\blacksquare\)

Resolvendo o Enscheidungsproblem

Lembra do “espirro” lá no início do post?

Chegou a hora de falarmos dele!!

Vamos começar entendendo o que tem a ver com o Problema da Parada com esse tal de Entscheidungsproblem ou Problema da Decisão…

Bem, o objetivo de Turing ao inventar as máquina universais foi justamente resolver o Entscheidungsproblem. Em seu artigo, Turing apenas menciona algo parecido com o Problema da Parada, mas não chega a resolvê-lo exatamente.

De todo modo, pelo menos na computação, o Problema da Parada acabou ficando mais famoso que o Problema da Decisão, e por isso muitas vezes se fala do primeiro sem sequer mencionar o segundo.

A grande sacada do Problema da Parada é que vários problemas são, na realidade, variações dele. Ou seja, se você conseguir resolver algum desses problemas, então você também consegue resolver o Problema da Parada. Como o Problema da Parada não tem solução, então você já sabe que o problema em questão também não tem.

Inclusive, podemos seguir exatamente a mesma lógica com o Entscheidungsproblem, quer ver?

Assuma que existe uma Máquina de Turing \(T\) capaz de decidir se uma determinada fórmula da lógica de predicados é satisfazível.

Seja \(P(M,i)\) a seguinte proposição: dada a entrada \(i\), a máquina \(M\) para.

Com a Máquina \(T\) nós sabemos exatamente se \(P(M,i)\) é satisfazível ou não, isto é, sabemos se \(M\) para ou não com uma entrada \(i\) qualquer.

Ué, então nós resolvemos o Problema da Parada.

Isso é, obviamente, uma contradição, pois já provamos que o Problema da Parada não tem solução. Logo, nossa hipótese de que existe um procedimento capaz de decidir a lógica de predicados (a máquina \(T\)) é falsa!

​\(\blacksquare\)

Conclusão

Assim nós fechamos as provas e as explicações sobre o Problema da Parada e o Enscheidungsproblem.

Só ficou faltando mostrar a prova daqueles exemplos impossíveis do começo do artigo. Mas eles são simples, é só utilizar a mesma técnica utilizada para demonstrar o Enscheidungsproblem. Vou deixá-las como dever de casa para ti enquanto não sai o próximo post.

Espero, sinceramente, que você tenha gostado e aprendido coisas novas.

Se você tiver qualquer dúvida, sugestão ou pedido de conteúdo, use o espaço de comentários abaixo e deixe uma mensagem para a gente.

Se você encontrou algum erro no meu desenvolvimento, por favor, sinta-se livre e encorajado para indicar.

Acho que é isso.

Até o próximo post!